称一张无标号无向简单图 $G$ 为“无禅”的,如果任何两种不同的给 $G$ 的点标号的方法得到的图都不同。
例如,下图不是无禅的,因为它有两种不同的给点的标号方法得到的图是相同的。
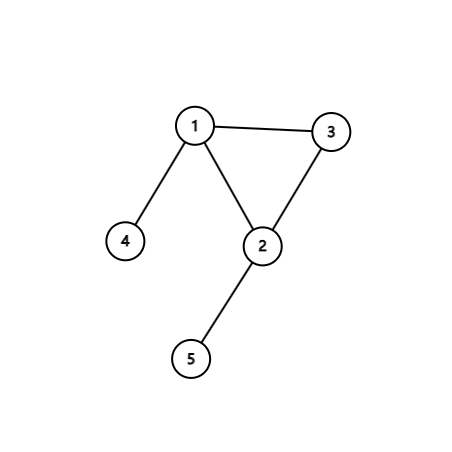
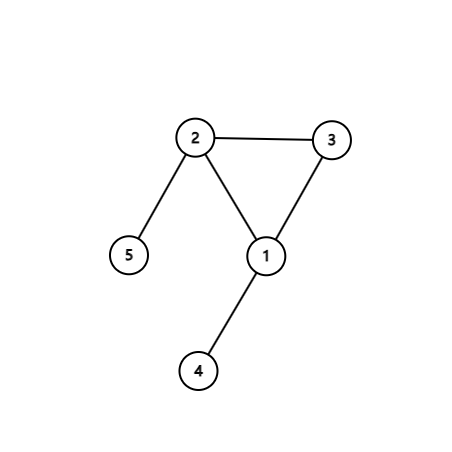
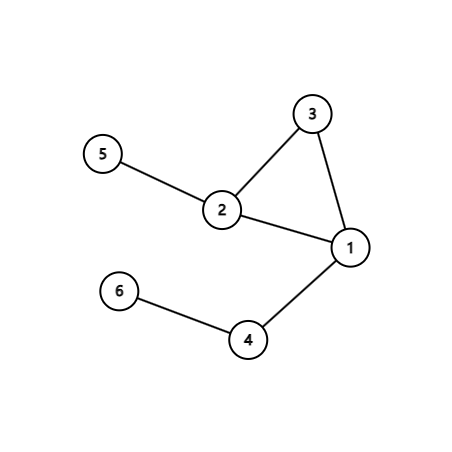
而下图是无禅的。
对于一张有 $n$ 个点,$m$ 条边的无标号无向简单图 $G(V,E)$ ,在给它的点标号为 $1$ 到 $n$ ,边标号为 $1$ 到 $m$ ,并将每条边定向后,我们可以用一个长为 $2m + 1$ 的序列 $m, u_1, v_1, u_2, v_2, \cdots, u_m, v_m$ 来表示这张图,即这张图有 $m$ 条边,第 $i$ 条边是从 $u_i$ 到 $v_i$ 的一条边。称这样的一个序列是 $G$ 的一种表示。
给定 $n$ ,求所有 $n$ 个点的“无禅”图的表示中字典序最小的一个。保证在给定的数据范围下有解。
输入格式
一行,一个正整数 $n$ 。
输出格式
一行,表示字典序最小的一个表示。
样例1
6
6 1 2 1 3 1 4 2 3 2 5 4 6
样例2
7
6 1 2 1 3 1 4 2 3 2 5 4 6
样例3
8
6 1 2 1 3 1 4 2 5 3 6 5 7
样例4
见下发文件。
数据范围
保证 $6\leq n\leq 5\times 10^5$ 。
| 测试点编号 | $n\leq$ |
|---|---|
| 1-2 | $10$ |
| 3-7 | $20$ |
| 8-11 | $100$ |
| 12-15 | $1000$ |
| 16-20 | $10^5$ |
| 21-25 | $5\times 10^5$ |
